Building my own robo-advisor

Back in 2019, I was using Charles Schwab Brokerage as my main investment account. They had a product called “Schwab Intelligent Advisors” – basically a robo-advising product. While I did not pay any management fees, the product was investing my money in an unnecessarily conservative manner. For the sake of interest income, Schwab was keeping a large amount of my long-term portfolio in cash.

As my investment horizon was ~40 years, I decided this was a bad idea. , I wrote my own version of a more aggressive robo-advisor to solve this problem.

The code for this project can be found on Github.

Technologies Used:

Python
Numpy
Pandas
CVXPY (Python convex optimization solver)
Yahoo Finance API

Problem Formulation

The general investment problem is: “I have a pot of money. How do I invest this pot of money?”. More formally, you have a fixed pool of funds you want to invest, and you do so by investing in asset classes via securities that belong to those asset classes.

We begin with a vector of Asset Classes, $A$ and target percent allocations for each Asset Class where $A_{i}$ is the target percent of the portfolio to be allocated to asset class $i$ . Therefore,

$\sum{A} = 1$

Each Asset Class will have securities associated with it. We define a Security-Asset Matrix, $S$ such that $S[x,y]$ identifies whether Security, $x$ belongs to Asset Class, $y$ . Each element in this matrix will be binary.

Furthermore, we must have a price vector $Pr$ where $Pr[i]$ is the current price of the security $i$ and an ownership vector, $O$ where $O[i]$ is how many shares of Security $i$ that you own. Also, we define a variable $C$ which defines the dollars we are investing into this portfolio.

The following identities hold:

$O \cdot Pr = PortfolioMarketCapitalizationBeforeInvestment [1]$
$(O \cdot Pr) \times S = MarketCapitalizationPerAssetClass [2]$
$\sum {(O \cdot Pr) \times S} = PortfolioMarketCapitalization [3]$
$[O \times Pr + C] = MarketCapitalizationIfAllAdditionalFundsAreInvested [4]$

Finally, we denote a diagonal matrix $Pu$ showing security purchases. This matrix will look like this:

$\begin{bmatrix} Pu_{1} & & \\ & \ddots & \\ & & Pu_{i} \end{bmatrix}$

Where $Pu_{i}$ shows we bought $Pu_{i}$ shares of security $i$

Cost Function

Let’s say you want to contribute, $F$ dollars to your portfolio. You want to invest in such a way that the securities you buy move the portfolio closer to the asset class percent allocation.

You can define a cost function like the following:

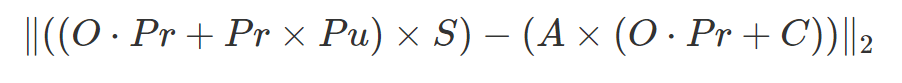
Here is a quick explainer of all the terms:

Effectively, this the sum of the squared differences between the dollar amount if you purchased a particular set of securities and the target allocation if you had a portfolio exactly meeting the pre-defined asset class allocation. The only variable here is $Pu$ . That’s what the optimizer will solve for.

Given this cost function, we can formulate the optimal security purchases as a Mixed Integer Quadratic Program (MIQP) with constraints. This has the excellent property of being a convex function.

Constraints

By adding constraints to this MIQP, we can better model the real world

Matrix $Pu$ must be diagonal. The matrix multiplication wouldn’t make sense without that.
No Fractional Securities –I cannot purchase fractional shares of the security
No Short Selling – I cannot sell more securities than I own
Max Investment Amount – I cannot invest more money than I have.
Max Uninvested Amount – Maximum Cash position after all trades are completed. I don’t want to be sitting on tons of cash after my trades are done.

Buy Only (Optional) – To avoid a taxable income event, I don’t want to be selling securities to achieve a greater portfolio balance in my general brokerage portfolio. I don’t have to worry about this in my Roth IRA, so this is an optional parameter.

Using that formulation, I built a Python app that runs the search. You can check it out here.

Next Steps

Storage

I’m not too happy with how the portfolio is stored and tracked at the moment. Right now, I just have some json files checked into my Git repo (omitted from the public repo for privacy reasons). While this is okay because it’s just a simple application for me, this isn’t the cleanest solution.

The better solution would be a database where I track the current portfolio holdings & transactions. I could build more features from this data set (tax loss harvesting) and I could also build a web app so other people can use this. Not worth the effort right now, but maybe in the future.

Ali Prasla